导数公式及运算法则有什么

导数在数学中属于比较难的知识点，那么怎样才能学好导数呢，下面小编为大家提供导数公式以及倒数的运算法则，仅供大家参考。

什么是导数

导数（Derivative）是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df(x0)/dx。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

常见的导数公式

基本初等函数导数公式主要有以下

y=f(x)=c (c为常数),则f'(x)=0

f(x)=x^n (n不等于0) f'(x)=nx^(n-1) (x^n表示x的n次方)

f(x)=sinx f'(x)=cosx

f(x)=cosx f'(x)=-sinx

f(x)=a^x f'(x)=a^xlna(a>0且a不等于1,x>0)

f(x)=e^x f'(x)=e^x

f(x)=logaX f'(x)=1/xlna (a>0且a不等于1,x>0)

f(x)=lnx f'(x)=1/x (x>0)

f(x)=tanx f'(x)=1/cos^2 x

f(x)=cotx f'(x)=- 1/sin^2 x

导数运算法则如下

(f(x)+/-g(x))'=f'(x)+/- g'(x)

(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)

(g(x)/f(x))'=(f(x)'g(x)-g(x)f'(x))/(f(x))^2

导数的求导法则

由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下：

1、求导的线性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合（即①式）。

2、两个函数的乘积的导函数：一导乘二+一乘二导（即②式）。

3、两个函数的商的导函数也是一个分式：（子导乘母-子乘母导）除以母平方（即③式）。

4、如果有复合函数，则用链式法则求导。

高阶导数的求法

1．直接法：由高阶导数的定义逐步求高阶导数。

一般用来寻找解题方法。

2．高阶导数的运算法则：

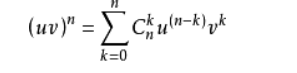
（二项式定理）

3．间接法：利用已知的高阶导数公式，通过四则运算，变量代换等方法。

注意：代换后函数要便于求，尽量靠拢已知公式求出阶导数。