2018年安徽高考数学模拟冲刺试题【含答案】
一、选择题:(本大题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合A={y|y=2x﹣1,x∈R},B={x|x2﹣x﹣2<0},则( )
A.﹣1∈A B.![]() ∉B C.A∩(∁RB)=A D.A∪B=A
∉B C.A∩(∁RB)=A D.A∪B=A
2.设i是虚数单位,复数![]() (a∈R)在平面内对应的点在直线方程x﹣y+1=0上,则a=( )
(a∈R)在平面内对应的点在直线方程x﹣y+1=0上,则a=( )
A.﹣1 B.0 C.1 D.2
 7.圆柱挖去两个全等的圆锥所得几何体的三视图如图所示,则其表面积为( )
7.圆柱挖去两个全等的圆锥所得几何体的三视图如图所示,则其表面积为( )
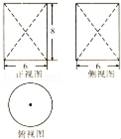
A.30π B.48π C.66π D.78π
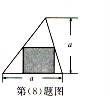
8.在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )

二、填空题:本大题共4小题,每小题5分

三、解答题.
 18.随着智能手机的发展,微信越来越成为人们交流的一种方式.某机构对使用微信交流的态度进行调查,随机调查了 50 人,他们年龄的频数分布及对使用微信交流赞成人数如表.
18.随着智能手机的发展,微信越来越成为人们交流的一种方式.某机构对使用微信交流的态度进行调查,随机调查了 50 人,他们年龄的频数分布及对使用微信交流赞成人数如表.
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(I)由以上统计数据填写下面 2×2 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 |
赞成 |
|
|
|
不赞成 |
|
|
|
合计 |
|
|
|
(Ⅱ)若对年龄在[55,65),[65,75)的被调查人中随机抽取两人进行追踪调查,记选中的4人中赞成使用微信交流的人数为X,求随机变量X的分布列和数学期望
参考公式:K2=![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
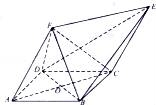
19.如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.
(Ⅰ)求证:BD⊥平面ACEF;
(Ⅱ)若∠DAB=60°,AF=FC,求二面角B﹣EC﹣D的正弦值.

请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-1:几何证明选讲]
22.如图,AB为⊙O的直径,C为⊙O上一点(异于A、B),AD与过点C的切线互相垂直,垂足为D,AD交⊙O于点P,过点B的切线交直线DC于点T.
(Ⅰ)证明:BC=PC;
(Ⅱ)若∠BTC=120°,AB=4,求DP•DA的值.
[选修4-4:坐标系与参数方程]
23.在平面直角坐标系xOy中,曲线C1的参数方程为![]() (φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(3,
(φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(3,![]() ),半径为1的圆.
),半径为1的圆.
(Ⅰ)求曲线C1,C2的直角坐标方程;
(Ⅱ)设M为曲线C1上的点,N为曲线C2上的点,求|MN|的取值范围.
[选修4-5:不等式选讲]
24.设函数f(x)=|x+2|+|x﹣2|,x∈R.
(Ⅰ)求不等式f(x)≤6的解集;
(Ⅱ)若关于x的方程f(x)=a|x﹣1|恰有两个不同的实数根,求a的取值范围.
2018年安徽高考数学模拟冲刺试题【含答案】
一、选择题:(本大题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合A={y|y=2x﹣1,x∈R},B={x|x2﹣x﹣2<0},则( )
A.﹣1∈A B.![]() ∉B C.A∩(∁RB)=A D.A∪B=A
∉B C.A∩(∁RB)=A D.A∪B=A
【考点】交、并、补集的混合运算.
【分析】化简集合A、B,即可得出结论A∪B=A.
【解答】解:∵A={y|y=2x﹣1,x∈R}={y|y>﹣1}=(﹣1,+∞),
B={x|x2﹣x﹣2<0}={x|﹣1<x<2}=(﹣1,2);
∴A∪B=A.
故选:D.
2.设i是虚数单位,复数![]() (a∈R)在平面内对应的点在直线方程x﹣y+1=0上,则a=( )
(a∈R)在平面内对应的点在直线方程x﹣y+1=0上,则a=( )
A.﹣1 B.0 C.1 D.2
【考点】复数的代数表示法及其几何意义.
【分析】利用复数代数形式的乘除运算化简,求出复数![]() (a∈R)在平面内对应的点的坐标,代入直线方程求解.
(a∈R)在平面内对应的点的坐标,代入直线方程求解.
【解答】解:∵![]() =
=![]() ,
,
∴![]() ,解得:a=﹣1.
,解得:a=﹣1.
故选:A.
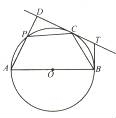
3.下列函数满足“∀x∈R,f(x)+f(﹣x)=0,且f′(x)≤0”的是( )
A.f(x)=x2|x| B.f(x)=﹣xe|x|
C.f(x)=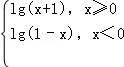 D.f(x)=x+sinx
D.f(x)=x+sinx
【考点】全称命题.
【分析】满足“∀x∈R,f(x)+f(﹣x)=0,且f′(x)≤0”的函数为奇函数,且在R上为减函数,进而得到答案.
【解答】解:满足“∀x∈R,f(x)+f(﹣x)=0,且f′(x)≤0”的函数为奇函数,且在R上为减函数,
A中函数f(x)=x2|x|,满足f(﹣x)=f(x),故函数为偶函数,
B中函数f(x)=﹣xe|x|,满足f(﹣x)=﹣f(x),即函数为奇函数,
且f′(x)=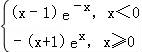 ≤0恒成立,故在R上为减函数,
≤0恒成立,故在R上为减函数,
C中函数f(x)=![]() ,满足f(﹣x)=f(x),故函数为偶函数;
,满足f(﹣x)=f(x),故函数为偶函数;
D中函数f(x)=x+sinx,满足f(﹣x)=﹣f(x),即函数为奇函数,但f′(x)=1+cosx≥0,在R上是增函数,
故选:B.
4.已知等差数列{an}的前n项和为Sn,公差为d,若![]() ﹣
﹣![]() =100,则d的值为( )
=100,则d的值为( )
A.![]() B.
B.![]() C.10 D.20
C.10 D.20
【考点】等差数列的性质.
【分析】![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() =1000d,即可得出.
=1000d,即可得出.
【解答】解:∵100=![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() =1000d,
=1000d,
解得d=![]() .
.
故选:B.
5.已知双曲线C:![]() ﹣
﹣![]() =1(b>0)的离心率为2,则C上任意一点到两条渐近线的距离之积为( )
=1(b>0)的离心率为2,则C上任意一点到两条渐近线的距离之积为( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
【考点】双曲线的简单性质.
【分析】利用点到直线的距离公式,结合双曲线方程,即可得出结论.
【解答】解:∵双曲线的离心率是2,
∴e2=![]() =
=![]() =4,得b=6,
=4,得b=6,
则双曲线方程为![]() ﹣
﹣![]() =1,渐近线方程为y=±
=1,渐近线方程为y=±![]() x,即x±
x,即x±![]() y=0,
y=0,
则C上任意一点P(x,y)到两条渐近线的距离之积为d1d2=![]() =
=![]() =
=![]() =
=![]() ,
,
故选:B
6.若α∈(0,![]() ),且cos2α+cos(
),且cos2α+cos(![]() +2α)=
+2α)=![]() ,则tanα( )
,则tanα( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】同角三角函数基本关系的运用.
【分析】由条件利用诱导公式、二倍角公式,同角三角函数的基本关系求得3tan2α+20tanα﹣7=0,解方程求得tanα的值.
【解答】解:若![]() ,且
,且![]() ,则cos2α﹣sin2α=
,则cos2α﹣sin2α=![]() (cos2α+sin2α),
(cos2α+sin2α),
∴![]() cos2α﹣
cos2α﹣![]() sin2α﹣2sinαcosα=0,即 3tan2α+20tanα﹣7=0.
sin2α﹣2sinαcosα=0,即 3tan2α+20tanα﹣7=0.
求得tanα=![]() ,或 tanα=﹣7(舍去),
,或 tanα=﹣7(舍去),
故选:B.
7.圆柱挖去两个全等的圆锥所得几何体的三视图如图所示,则其表面积为( )
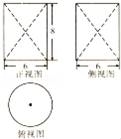
A.30π B.48π C.66π D.78π
【考点】由三视图求面积、体积.
【分析】利用三视图的数据直接求解几何体的表面积即可.
【解答】解:由三视图可知几何体的表面积为![]() =78π.
=78π.
故选:D.
8.在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】几何概型.
【分析】设矩形的长为x,宽为y,由三角形相似可得y=a﹣x,由基本不等式可得矩形的最大面积,可得最大概率.
【解答】解:设矩形的长为x,宽为y,
则由三角形相似可得![]() =
=![]() ,解得y=a﹣x,
,解得y=a﹣x,
∴矩形的面积S=xy=x(a﹣x)≤![]() =
=![]() ,
,
当且仅当x=a﹣x即x=![]() 时,S取最大值
时,S取最大值![]() ,
,
∴点落入矩形内的最大概率为 =
=![]() ,
,
故选:C.
9.执行如图所示程序框图,输出的a=( )
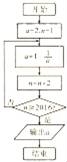
A.﹣1 B.![]() C.1 D.2
C.1 D.2
【考点】循环结构.
【分析】模拟程序框图的运行过程,即可得出a的取值是以3为周期而变化的,从而得出程序运行后输出的a值.
【解答】解:由程序框图可得a=2,n=1,
a=![]() ,n=3,
,n=3,
a=﹣1,n=5,
a=2,n=7,
a=![]() ,n=9,…
,n=9,…
∴a的取值是以3为周期而变化的,
∴a=2,n=2017.
故选:D.
10.已知x,y满足约束条件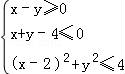 ,则z=﹣
,则z=﹣![]() x+y的最小值为( )
x+y的最小值为( )
A.﹣2![]() B.﹣
B.﹣![]() C.0 D.
C.0 D.![]()
【考点】简单线性规划.
【分析】作出平面区域,移动目标函数,观察图形寻找最优解的位置.
【解答】解:作出平面区域如图:
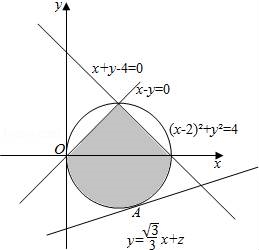
由z=﹣![]() x+y得y=
x+y得y=![]() x+z,
x+z,
由图可知当y=![]() x+z与圆(x﹣2)2+y2=4相切时,z取得最小值.
x+z与圆(x﹣2)2+y2=4相切时,z取得最小值.
把y=![]() x+z化成一般式方程为
x+z化成一般式方程为![]() x﹣3y+3z=0,
x﹣3y+3z=0,
∴![]() =2,解得z=﹣2
=2,解得z=﹣2![]() 或z=
或z=![]() (舍).
(舍).
故选:A.
11.已知函数f(x)=asinx﹣![]() cosx的一条对称轴为x=﹣
cosx的一条对称轴为x=﹣![]() ,且f(x1)•f(x2)=﹣4,则下列结论正确的是( )
,且f(x1)•f(x2)=﹣4,则下列结论正确的是( )
A.a=±1 B.f(x1+x2)=0
C.|x1+x2|的最小值为![]() D.f(x)的最小正周期为2|x1﹣x2|
D.f(x)的最小正周期为2|x1﹣x2|
【考点】三角函数中的恒等变换应用;正弦函数的图象.
【分析】首先通过三角函数的恒等变换把函数关系式变性成正弦型函数,进一步利用对称轴确定函数的解析式,再利用正弦型函数的最值确定结果.
【解答】解:f(x)=asinx﹣![]() cosx
cosx
=![]() sin(x+θ),
sin(x+θ),
由于函数的对称轴为:x=﹣![]() ,
,
所以f(﹣![]() )=﹣
)=﹣![]() a﹣
a﹣![]() ,
,
则:|﹣![]() a﹣
a﹣![]() |=
|=![]() ,
,
解得:a=1,
所以:f(x)=2sin(x﹣![]() ),
),
由于:f(x1)•f(x2)=﹣4,
所以函数必须取得最大值和最小值,
所以:x1=2kπ+![]() 或x2=2kπ﹣
或x2=2kπ﹣![]() ,
,
所以:|x1+x2|=4kπ+![]() ,当k=0时,最小值为
,当k=0时,最小值为![]() .
.
故选:C.
12.已知![]() <a<4,函数f(x)=x3﹣3bx2+a有且仅有两个不同的零点x1,x2,则|x1﹣x2|的取值范围是( )
<a<4,函数f(x)=x3﹣3bx2+a有且仅有两个不同的零点x1,x2,则|x1﹣x2|的取值范围是( )
A.(![]() ,1) B.(1,2) C.(
,1) B.(1,2) C.(![]() ,3) D.(2,3)
,3) D.(2,3)
【考点】函数零点的判定定理.
【分析】处理一元三次函数的零点问题可借助其导函数.如本题有两个不同的零点即为其导函数有两个不同的根.
【解答】解:∵函数f(x)有且仅有两个不同的零点,
∴f(x)的导函数f′(x)=3x2﹣6bx,有两个不同的根
由f′(x)=0得x=0或x=2b
∵f(0)=a≠0,
∴f(2b)=0,即![]() <b<1
<b<1
则f(x)有一根是确定的,为2b.
f(x)的另一个根为负的,且f(x)=(x﹣2b)2(x+b)
∴另一个根为﹣b.
则|x1﹣x2|=3b
∴两个根的差的绝对值为(![]() ,3)
,3)
故选:C.
二、填空题:本大题共4小题,每小题5分
13.已知(![]() +y)(x+
+y)(x+![]() )5的展开式中
)5的展开式中![]() 的系数为20a,其中a≠0,则a的值为 ﹣2或1 .
的系数为20a,其中a≠0,则a的值为 ﹣2或1 .
【考点】二项式定理.
【分析】把(x+![]() )5按照二项式定理展开,可得已知(
)5按照二项式定理展开,可得已知(![]() +y)(x+
+y)(x+![]() )5的展开式中
)5的展开式中![]() 的系数,再根据中
的系数,再根据中![]() 的系数为20a,求得a的值.
的系数为20a,求得a的值.
【解答】解:(![]() +y)(a+
+y)(a+![]() )5=(
)5=(![]() +y)(
+y)(![]() •x5+
•x5+![]() •x4•
•x4•![]() +
+![]() •x3•
•x3•![]() +
+![]() •x2•
•x2•![]() +
+![]() •ax
•ax![]() +
+![]() •
•![]() ),
),
故(![]() +y)(a+
+y)(a+![]() )5的展开式中
)5的展开式中![]() 的系数为
的系数为![]() •a2+
•a2+![]() •a3=20a,
•a3=20a,
即a2+a﹣2=0,求得a=﹣2或a=1,
故答案为:﹣2或1.
14.已知向量![]() 在向量
在向量![]() =(1,
=(1,![]() )方向上的投影为2,且|
)方向上的投影为2,且|![]() ﹣
﹣![]() |=
|=![]() ,则|
,则|![]() |= 3 .
|= 3 .
【考点】平面向量数量积的坐标表示、模、夹角.
【分析】根据条件可以求得![]() ,而对
,而对![]() 两边平方便可得到
两边平方便可得到![]() ,这样即可求出
,这样即可求出![]() 的值.
的值.
【解答】解:由已知得:![]() ,
,![]() ;
;
∴![]() ;
;
∴由![]() 得,
得,![]() ;
;
∴![]() ;
;
∴![]() .
.
故答案为:3.
15.已知抛物线C:y2=6x的焦点为F,B为C的准线上一点,A为直线BF与C的一个交点,若![]() =3
=3![]() ,则点A到原点的距离为
,则点A到原点的距离为 ![]() .
.
【考点】抛物线的简单性质.
【分析】求得抛物线的焦点和准线方程,设B(﹣![]() ,m),A(s,t),运用向量共线的坐标表示,解方程可得A的坐标,由两点的距离公式计算即可得到所求值.
,m),A(s,t),运用向量共线的坐标表示,解方程可得A的坐标,由两点的距离公式计算即可得到所求值.
【解答】解:y2=6x的焦点为F(![]() ,0),准线方程为x=﹣
,0),准线方程为x=﹣![]() ,
,
设B(﹣![]() ,m),A(s,t),由
,m),A(s,t),由![]() =3
=3![]() ,可得﹣
,可得﹣![]() ﹣
﹣![]() =3(s﹣
=3(s﹣![]() ),
),
解得s=![]() ,t=±
,t=±![]() ,
,
即有|OA|=![]() =
=![]() .
.
故答案为:![]() .
.
16.已知△ABC中,AB+![]() AC=6,BC=4,D为BC的中点,则当AD最小时,△ABC的面积为
AC=6,BC=4,D为BC的中点,则当AD最小时,△ABC的面积为 ![]() .
.
【考点】余弦定理的应用;三角形的面积公式.
【分析】根据余弦定理可得:AC2=AD2+22﹣4AD•cos∠ADC,且![]() ,进而
,进而![]() ,结合二次函数的图象和性质,可得AC=2
,结合二次函数的图象和性质,可得AC=2![]() 时,AD取最小值
时,AD取最小值![]() ,由余弦定理求出cos∠ACB,进而求出sin∠ACB,代入三角形面积公式,可得答案.
,由余弦定理求出cos∠ACB,进而求出sin∠ACB,代入三角形面积公式,可得答案.
【解答】解:∵AB+![]() AC=6,BC=4,D为BC的中点,
AC=6,BC=4,D为BC的中点,
根据余弦定理可得:AC2=AD2+CD2﹣2AD•CD•cos∠ADC,且AB2=AD2+BD2﹣2AD•BD•cos∠ADB,
即AC2=AD2+22﹣4AD•cos∠ADC,且![]() ,
,
∵∠ADB=π﹣∠ADC,
∴![]() ,
,
∴![]() ,
,
当AC=2![]() 时,AD取最小值
时,AD取最小值![]() ,
,
此时cos∠ACB=![]() =
=![]() ,
,
∴sin∠ACB=![]() ,
,
∴△ABC的面积S=![]() AC•BC•sin∠ACB=
AC•BC•sin∠ACB=![]() ,
,
故答案为:![]() .
.
三、解答题.
17.已知数列{an}的前n项和为Sn,且a1=3,Sn+1﹣2Sn=1﹣n,n∈N*.
(1)求数列{an}的通项公式;
(2)证明:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() .
.
【考点】数列的求和;数列递推式.
【分析】(1)Sn+1﹣2Sn=1﹣n,n∈N*.可得Sn+1﹣(n+1)=2(Sn﹣n),利用等比数列的通项公式可得Sn,再利用递推关系可得an.
(2)当n=1时,![]() =
=![]()
![]() 成立.当n≥2时,
成立.当n≥2时,![]() =
=![]() <
<![]() .再利用等比数列的前n项和公式、不等式的性质即可得出.
.再利用等比数列的前n项和公式、不等式的性质即可得出.
【解答】(1)解:∵Sn+1﹣2Sn=1﹣n,n∈N*.
∴Sn+1﹣(n+1)=2(Sn﹣n),
∴数列{Sn﹣n}是等比数列,首项为2,公比为2.
∴Sn﹣n=2n,
∴Sn=2n+n.
当n≥2时,an=Sn﹣Sn﹣1=2n+n﹣(2n﹣1+n﹣1)=2n﹣1+1.
∴an=![]() .
.
(2)证明:当n=1时,![]() =
=![]()
![]() 成立.
成立.
当n≥2时,![]() =
=![]() <
<![]() .
.
∴![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() +
+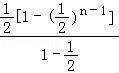 =
=![]() ﹣
﹣![]() <
<![]() .
.
18.随着智能手机的发展,微信越来越成为人们交流的一种方式.某机构对使用微信交流的态度进行调查,随机调查了 50 人,他们年龄的频数分布及对使用微信交流赞成人数如表.
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(I)由以上统计数据填写下面 2×2 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 |
赞成 |
|
|
|
不赞成 |
|
|
|
合计 |
|
|
|
(Ⅱ)若对年龄在[55,65),[65,75)的被调查人中随机抽取两人进行追踪调查,记选中的4人中赞成使用微信交流的人数为X,求随机变量X的分布列和数学期望
参考公式:K2=![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
【考点】独立性检验的应用;离散型随机变量的期望与方差.
【分析】(I)根据题目中的数据填写列联表,利用公式计算K2,对照数表即可得出结论;
(Ⅱ)根据题意得出X的所有可能取值,计算对应的概率值,写出X的分布列与数学期望值.
【解答】解:(I)由以上统计数据填写下面 2×2 列联表,如下;
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 |
赞成 | 10 | 27 | 37 |
不赞成 | 10 | 3 | 13 |
合计 | 20 | 30 | 50 |
根据公式计算K2=![]() =
=![]() ≈9.98>6.635,
≈9.98>6.635,
所以有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
(Ⅱ)根据题意,X的所有可能取值为0,1,2,3,
则P(X=0)=![]() •
•![]() =
=![]() ×
×![]() =
=![]() ,
,
P(X=1)=![]() •
•![]() +
+![]() •
•![]() =
=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() ,
,
P(X=2)=![]() •
•![]() +
+![]() •
•![]() =
=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() ,
,
P(X=3)=![]() •
•![]() =
=![]() ×
×![]() =
=![]() ;
;
随机变量X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以X的数学期望为EX=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() =
=![]() .
.
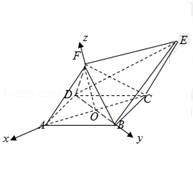
19.如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.
(Ⅰ)求证:BD⊥平面ACEF;
(Ⅱ)若∠DAB=60°,AF=FC,求二面角B﹣EC﹣D的正弦值.
【考点】用空间向量求平面间的夹角;直线与平面垂直的判定.
【分析】(Ⅰ)由已知得BD⊥AC,BD⊥OF,由此能证明BD⊥平面ACEF.
(Ⅱ)由已知得AC⊥OF,OF⊥平面ABCD,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角B﹣EC﹣D的正弦值.
【解答】证明:(Ⅰ)∵ABCD为菱形,∴BD⊥AC,
∵O为AC与BD的交点,∴O为BD的中点,
又△BDF为等边三角形,∴BD⊥OF,
∵AC⊂平面ACEF,OF⊂平面ACEF,AC∩OF=O,
∴BD⊥平面ACEF.
(Ⅱ)∵AF=FC,O为AC中点,∴AC⊥OF,
∵BD⊥OF,∴OF⊥平面ABCD,
建立空间直角坐标系O﹣xyz,不妨设AB=2,
∵∠DAB=60°,∴B(0,1,0),C(﹣![]() ,0,0),
,0,0),
D(0,﹣1,0),A(![]() ,0,0),F(0,0,
,0,0),F(0,0,![]() ),
),
∵![]() =
=![]() ,∴E(﹣2
,∴E(﹣2![]() ,0,
,0,![]() ),
),
![]() =(﹣
=(﹣![]() ,﹣1,0),
,﹣1,0),![]() =(﹣2
=(﹣2![]() ,﹣1,
,﹣1,![]() ),
),
设![]() =(x,y,z)为平面BEC的法向量,
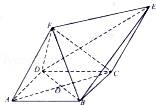
=(x,y,z)为平面BEC的法向量,
则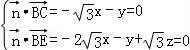 ,
,
取x=1,得![]() =(1,﹣
=(1,﹣![]() ,1),
,1),
则理求得平面ECD的法向量![]() =(1,
=(1,![]() ,1),
,1),
设二面角B﹣EC﹣D的平面角为θ,
则cosθ=![]() =
=![]() ,
,
∴sinθ=![]() =
=![]() ,
,
∴二面角B﹣EC﹣D的正弦值为![]() .
.
20.已知点M(x,y)到点F(2,0)的距离与定直线x=![]() 的距离之比为
的距离之比为![]() ,设点M的轨迹为曲线E
,设点M的轨迹为曲线E
(Ⅰ)求曲线E的方程;
(Ⅱ)设F关于原点的对称点为F′,是否存在经过点F的直线l交曲线E与A、B两点,使得△F′AB的面积为![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
【考点】直线与圆锥曲线的综合问题.
【分析】(I)运用两点的距离公式和点到直线的距离公式,化简整理,可得曲线E的方程;
(Ⅱ)假设存在经过点F的直线l交曲线E于A、B两点,且三角形F′AB的面积为![]() .设直线l:x=my+2,代入椭圆方程x2+5y2=5,运用韦达定理,由三角形的面积公式可得
.设直线l:x=my+2,代入椭圆方程x2+5y2=5,运用韦达定理,由三角形的面积公式可得![]() •4•|y1﹣y2|=
•4•|y1﹣y2|=![]() ,化简整理计算即可得到所求直线的方程.
,化简整理计算即可得到所求直线的方程.
【解答】解:(I)由题意可得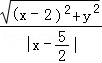 =
=![]() ,
,
移项两边平方可得,x2+y2﹣4x+4=![]() x2﹣4x+5,
x2﹣4x+5,
即有曲线E的轨迹方程为![]() +y2=1;
+y2=1;
(Ⅱ)假设存在经过点F(2,0)的直线l交曲线E于A、B两点,
且三角形F′AB的面积为![]() .
.
由题意可得F'(﹣2,0),设直线l:x=my+2,
代入椭圆方程x2+5y2=5,可得
(5+m2)y2+4my﹣1=0,
设直线l交椭圆E于A(x1,y1)、B(x2,y2)两点,
可得y1+y2=﹣![]() ,y1y2=﹣
,y1y2=﹣![]() ,
,
|y1﹣y2|=![]() =
=![]() =
=![]() ,
,
由三角形F′AB的面积为![]() ,可得
,可得![]() •4•|y1﹣y2|=
•4•|y1﹣y2|=![]() ,
,
即有![]() =
=![]() ,解得m=±
,解得m=±![]() ,
,
可得存在直线l,且方程为x=±![]() y+2.
y+2.
21.设函数f(x)=ex﹣ax2﹣2x﹣1.
(1)若曲线y=f(x)在点(1,f(1))处的切线为l,且l在y轴上的截距为﹣2,求实数a的值;
(2)若1<a<2,证明:存在x0∈(﹣![]() ,﹣
,﹣![]() ),使得f′(x0)=0,且f(x0)<
),使得f′(x0)=0,且f(x0)<![]() .
.
【考点】利用导数研究曲线上某点切线方程;导数的运算.
【分析】(1)求出导数,求得切线的斜率和切点,再由两点的斜率公式,解方程可得a的值;
(2)求出导数,求得f′(﹣![]() )>0,f′(﹣
)>0,f′(﹣![]() )<0在1<a<2成立,运用零点存在定理可得存在x0∈(﹣
)<0在1<a<2成立,运用零点存在定理可得存在x0∈(﹣![]() ,﹣
,﹣![]() ),使得f′(x0)=0;再由f(x0)﹣
),使得f′(x0)=0;再由f(x0)﹣![]() =﹣ax02+(2a﹣2)x0+
=﹣ax02+(2a﹣2)x0+![]() ,求出对称轴和区间的关系,求得端点的函数值的符号,即可得证.
,求出对称轴和区间的关系,求得端点的函数值的符号,即可得证.
【解答】解:(1)函数f(x)=ex﹣ax2﹣2x﹣1的导数为f′(x)=ex﹣2ax﹣2,
在点(1,f(1))处的切线斜率为e﹣2a﹣2,
切点为(1,e﹣a﹣3),又切线过(0,﹣2),
则e﹣2a﹣2=![]() ,解得a=﹣1;
,解得a=﹣1;
(2)证明:由1<a<2,f′(﹣![]() )=
)=![]() +2﹣2>0,
+2﹣2>0,
f′(﹣![]() )=
)=![]() +
+![]() ﹣2<0在1<a<2成立,
﹣2<0在1<a<2成立,
由零点存在定理可得,
存在x0∈(﹣![]() ,﹣
,﹣![]() ),使得f′(x0)=0;
),使得f′(x0)=0;
且f′(x0)=ex0﹣2ax0﹣2=0,即ex0=2ax0+2,
可得f(x0)=ex0﹣ax02﹣2x0﹣1=﹣ax02+(2a﹣2)x0+1,
由f(x0)﹣![]() =﹣ax02+(2a﹣2)x0+
=﹣ax02+(2a﹣2)x0+![]() ,
,
对称轴为x0=![]() >0,区间(﹣
>0,区间(﹣![]() ,﹣
,﹣![]() )为增区间,
)为增区间,
由f(﹣![]() )=﹣
)=﹣![]() ﹣
﹣![]() (a﹣1)+
(a﹣1)+![]() =
=![]() (1﹣a)<0,
(1﹣a)<0,
又f(﹣![]() )>f(﹣
)>f(﹣![]() ),
),
则f(x0)在(﹣![]() ,﹣
,﹣![]() )都有f(x0)<
)都有f(x0)<![]() .
.
请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-1:几何证明选讲]
22.如图,AB为⊙O的直径,C为⊙O上一点(异于A、B),AD与过点C的切线互相垂直,垂足为D,AD交⊙O于点P,过点B的切线交直线DC于点T.
(Ⅰ)证明:BC=PC;
(Ⅱ)若∠BTC=120°,AB=4,求DP•DA的值.
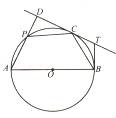
【考点】与圆有关的比例线段.
【分析】(Ⅰ)连接AC,BP,利用直径所对的圆周角为直角,圆的切线的性质,证明∠CBP=∠CPB,即可证明:BC=PC;
(Ⅱ)求出AC=2![]() ,DC=
,DC=![]() ,利用切割线定理求DP•DA的值.
,利用切割线定理求DP•DA的值.
【解答】(Ⅰ)证明:连接AC,BP,
∵AB是半圆O的直径,C为圆周上一点,∴∠ACB=90°,
即∠BCT+∠ACD=90°,
又∵AD⊥DC,∴∠DAC+∠ACD=90°,
∴∠BCT=∠DAC,
又∵直线DT是圆O的切线,∴∠CPB=∠BCT,
又∠DAC=∠CBP,∴∠CBP=∠CPB,∴BC=PC.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(Ⅱ)解:由题意知点A,B,T,D四点共圆,∴∠DAB=60°,
∴∠DAC=∠CAB=30°,
∴AC=2![]() ,DC=
,DC=![]()
∴DP•DA=DC2=3﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
[选修4-4:坐标系与参数方程]
23.在平面直角坐标系xOy中,曲线C1的参数方程为![]() (φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(3,
(φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(3,![]() ),半径为1的圆.
),半径为1的圆.
(Ⅰ)求曲线C1,C2的直角坐标方程;
(Ⅱ)设M为曲线C1上的点,N为曲线C2上的点,求|MN|的取值范围.
【考点】椭圆的参数方程;简单曲线的极坐标方程.
【分析】(Ⅰ)消去参数φ可得C1的直角坐标方程,易得曲线C2的圆心的直角坐标为(0,3),可得C2的直角坐标方程;
(Ⅱ)设M(2cosφ,sinφ),由三角函数和二次函数可得|MC2|的取值范围,结合圆的知识可得答案.
【解答】解:(Ⅰ)消去参数φ可得C1的直角坐标方程为![]() +y2=1,
+y2=1,
∵曲线C2是圆心为(3,![]() ),半径为1的圆
),半径为1的圆
曲线C2的圆心的直角坐标为(0,3),
∴C2的直角坐标方程为x2+(y﹣3)2=1;
(Ⅱ)设M(2cosφ,sinφ),则|MC2|=![]()
=![]() =
=![]()
=![]() ,
,
∴﹣1≤sinφ≤1,∴由二次函数可知2≤|MC2|≤4,
由题意结合图象可得|MN|的最小值为2﹣1=1,最大值为4+1=5,
∴|MN|的取值范围为[1,5]
[选修4-5:不等式选讲]
24.设函数f(x)=|x+2|+|x﹣2|,x∈R.
(Ⅰ)求不等式f(x)≤6的解集;
(Ⅱ)若关于x的方程f(x)=a|x﹣1|恰有两个不同的实数根,求a的取值范围.
【考点】绝对值不等式的解法;根的存在性及根的个数判断.
【分析】(Ⅰ)根据绝对值的意义,求得不等式f(x)≤6的解集.
(Ⅱ)函数f(x)的图象(图中红色部分)与直线 y=a|x﹣1|有2个不同的交点,数形结合可得a的范围.
【解答】解:(Ⅰ)函数f(x)=|x+2|+|x﹣2|表示数轴上的x
对应点到﹣2、2对应点的距离之和,
而3和﹣3对应点到﹣2、2对应点的距离之和正好等于6,
故不等式f(x)≤6的解集为{x|x≤﹣2,或x≥2}.
(Ⅱ)∵f(x)=|x+2|+|x﹣2|=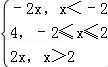 ,
,
∴f(x)≥4,
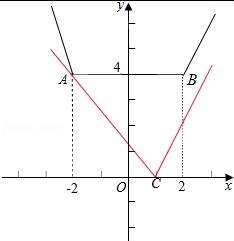
若关于x的方程f(x)=a|x﹣1|恰有两个不同的实数根,
则函数f(x)的图象与直线 y=a|x﹣1|(图中红色部分)
有2个不同的交点,如图所示:
由于A(﹣2,4)、B(2,4)、C(1,0),
∴﹣2<﹣a<KCA,或 a>KCB,即﹣2<﹣a<﹣![]() ,或a>4,
,或a>4,
求得![]() <a<2,或a>4.
<a<2,或a>4.
第19页(共19页)

2019山东高考文科文科数学科目的考试已经结束了,同学们都考的怎么样呢?小编为大家整理了2019年山东高考文科文科数学试卷,供大家参考。20...


安徽高考理科数学科目已经结束,小编为大家整理了安徽理科数学高考试卷,各位考生可以根据试卷预估一下自己的考试情况,为接下来的填报志愿等工作做准...


2019安徽高考文科数学科目的考试已经结束了,同学们都考的怎么样呢?小编为大家整理了2019年安徽高考文科数学试卷,供大家参考。2019年安...

2019安徽高考文科数学科目的考试已经结束了,同学们都考的怎么样呢?小编为大家整理了2019年安徽高考文科数学试卷,供大家参考。2019年安...

刚刚已经结束了2018高考数学考试,下文是小编给大家整理的最新出炉的2018年安徽高考理科数学试题真题图片版本,供参考!安徽2018高考理科...

2018年安徽高考理科数学模拟冲刺试题【含答案】

2018年安徽高考数学模拟试题【含答案】

2017年安徽高考理科数学模拟试题(含答案)