
2017年浙江高考数学试题答案解析【最新Word版】
本试题卷分选择题和非选择题两部分。全卷共4页,选择题部分1至2页,非选择题部分3至4页。满分150分。考试用时120分钟。
考生注意:
1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:
球的表面积公式 锥体的体积公式
![]()
![]()
球的体积公式 其中S表示棱锥的底面面积,h表示棱锥的高
![]() 台体的体积公式
台体的体积公式
其中R表示球的半径 ![]()
柱体的体积公式 其中Sa,Sb分别表示台体的上、下底面积
V=Sh h表示台体的高
其中S表示棱柱的底面面积,h表示棱柱的高
选择题部分(共40分)www.ccutu.com
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】取![]() 所有元素,得
所有元素,得![]()
![]() .
.
2.椭圆![]() 的离心率是
的离心率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】![]() ,选B.
,选B.
3.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是
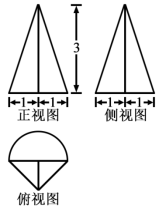
A.![]() +1 B.
+1 B.![]() +3 C.
+3 C.![]() +1D.
+1D.![]() +3
+3
【答案】A
【解析】![]() ,选A.
,选A.
4.若![]() ,
,![]() 满足约束条件
满足约束条件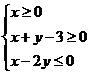 ,则z=x+2y的取值范围是
,则z=x+2y的取值范围是
A.[0,6] B.[0,4] C.[6,+∞] D.[4,+∞]
【答案】D
【解析】可行域为一开放区域,所以直线过点![]() 时取最小值4,无最大值,选D.
时取最小值4,无最大值,选D.
5.若函数f(x)=x2+ ax+b在区间[0,1]上的最大值是M,最小值是m,则M – m
A.与a有关,且与b有关 B.与a有关,但与b无关
C.与a无关,且与b无关 D.与a无关,但与b有关
【答案】B
【解析】因为最值在![]() 中取,所以最值之差一定与b无关,选B.
中取,所以最值之差一定与b无关,选B.
6.已知等差数列[an]的公差为d,前n项和为Sn,则“d>0”是“S4 + S6”>2S5的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】C
【解析】![]() ,所以为充要条件,选C.
,所以为充要条件,选C.
7.函数y=f(x)的导函数![]() 的图像如图所示,则函数y=f(x)的图像可能是
的图像如图所示,则函数y=f(x)的图像可能是
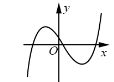
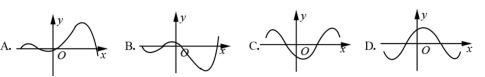
【答案】D
【解析】原函数先减再增,再减再增,因此选D.
8.已知随机变量![]() 1满足P(
1满足P(![]() =1)=pi,P(
=1)=pi,P(![]() =0)=1—pi,i=1,2.若0<p1<p2<
=0)=1—pi,i=1,2.若0<p1<p2<![]() ,则
,则
A.![]() <
<![]() ,
,![]() <
<![]() B.
B.![]() <
<![]() ,
,![]() >
>![]()
C.![]() >
>![]() ,
,![]() <
<![]() D.
D.![]() >
>![]() ,
,![]() >
>![]()
8.【答案】A
【解析】![]()
![]() ,选A.
,选A.
9.如图,已知正四面体D–ABC(所有棱长均相等的三棱锥),PQR分别为AB,BC,CA上的点,AP=PB,![]() ,分别记二面角D–PR–Q,D–PQ–R,D–QR–P的平面较为α,β,γ,则
,分别记二面角D–PR–Q,D–PQ–R,D–QR–P的平面较为α,β,γ,则
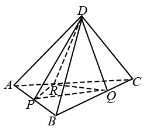
A.γ<α<β B.α<γ<β C.α<β<γ D.β<γ<α
【答案】B
【解析】设O为三角形ABC中心,则O到PQ距离最小,O到PR距离最大,O到RQ距离居中,而高相等,因此![]() 所以选B
所以选B
10.如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记![]() ,
,![]() ,
,![]() ,则
,则
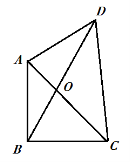
A.I1<I2<I3 B.I1<I3<I2 C. I3<I1<I2 D.I2<I1<I3
【答案】C
【解析】因为![]() ,所以
,所以![]()
选C
非选择题部分(共110分)www.ccutu.com
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度。祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S内,S内=。
【答案】![]()
【解析】将正六边形分割为6个等边三角形,则:![]()
12.已知ab∈R,![]() (i是虚数单位)学*科 网则
(i是虚数单位)学*科 网则![]() ,ab=。
,ab=。
【答案】5,2
【解析】由题意可得![]() ,则
,则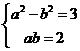 ,解得
,解得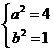 ,则
,则![]()
13.已知多项式![]() 1
1![]() 2=
2=![]() ,则
,则![]() =________________,
=________________,![]() =________.
=________.
【答案】16,4
【解析】由二项式展开式可得通项公式为:![]() ,分别取
,分别取![]() 和
和![]() 可得
可得![]() ,令
,令![]() 可得
可得![]()
14.已知△ABC,AB=AC=4,BC=2. 点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是______,cos∠BDC=_______.
【答案】![]()

15.已知向量a,b满足![]() 则
则![]() 的最小值是________,最大值是_______.
的最小值是________,最大值是_______.
【答案】4,![]()
【解析】设向量![]() 的夹角为
的夹角为![]() ,由余弦定理有:
,由余弦定理有:![]() ,
,
![]() ,则:
,则:
![]() ,
,
令![]() ,则
,则![]() ,
,
据此可得:![]() ,
,
即![]() 的最小值是4,最大值是
的最小值是4,最大值是![]() .
.
16.从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有______中不同的选法.(用数字作答)
【答案】660
【解析】由题意可得:总的选择方法为:![]() 种方法,其中不满足题意的选法有
种方法,其中不满足题意的选法有![]() 种方法,则满足题意的选法有:
种方法,则满足题意的选法有:![]() 种.
种.
17.已知α![]() R,函数f(x)=‖x+
R,函数f(x)=‖x+![]() ‖–α+α在区间[1,4]上的最大值是5,则α的取值范围是___________.
‖–α+α在区间[1,4]上的最大值是5,则α的取值范围是___________.
【答案】![]()

三、解答题:本大题共5小题,共74分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)已知函数f(x)=sin2x–cos2x–![]() sin x cos x(x
sin x cos x(x![]() R).
R).
(Ⅰ)求f(![]() )的值.
)的值.
(Ⅱ)求f(x)的最小正周期及单调递增区间.
【答案】(Ⅰ)2;(Ⅱ)最小正周期为![]() 单调递增区间为
单调递增区间为![]()
【解析】(Ⅰ)f(x)=![]()
=![]() 2
2![]()
则f(![]() )=
)=![]() 2
2![]()
(Ⅱ)f(x)的最小正周期为![]() .
.
令2![]()
函数f(x)的单调递增区间为![]()
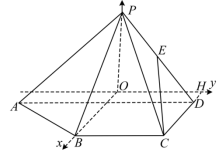
19.(本题满分15分)如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
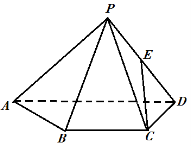
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】方法一:
(1)取AD的中点F,连接EF,CF
∵E为PD的重点
∴EF∥PA
在四边形ABCD中,BC∥AD,AD=2DC=2CB,F为中点
易得CF∥AB
∴平面EFC∥平面ABP
∵EC![]() 平面EFC
平面EFC
∴EC∥平面PAB
(2)连结BF,过F作FM⊥PB与M,连结PF
因为PA=PD,所以PF⊥AD
易知四边形BCDF为矩形,所以BF⊥AD
所以AD⊥平面PBF,又AD∥BC,所以BC⊥平面PBF,所以BC⊥PB
设DC=CB=1,则AD=PC=2,所以PB=![]() ,BF=PF=1
,BF=PF=1
所以MF=![]() ,又BC⊥平面PBF,所以BC⊥MF
,又BC⊥平面PBF,所以BC⊥MF
所以MF⊥平面PBC,即点F到平面PBC的距离为![]()
也即点D到平面PBC的距离为![]()
因为E为PD的中点,所以点E到平面PBC的距离为![]()
在△PCD中,PC=2,CD=1,PD=![]() ,由余弦定理可得CE=
,由余弦定理可得CE=![]()
设直线CE与平面PBC所成的角为θ,则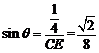
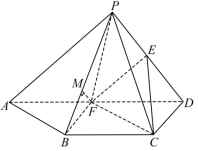
方法二
解:(1)略;构造平行四边形
(2)过P作PH⊥CD,交CD的延长线于点H
在Rt△PDH中,设DH=x,则易知![]() ,(Rt△PCH)
,(Rt△PCH)
解得DH=![]()
过H作BC的平行线,取DH=BC=1,
由题易得B(![]() ,0,0),D(
,0,0),D(![]() ,1,0),C(
,1,0),C(![]() ,1,0),P(0,0,
,1,0),P(0,0,![]() ),E(
),E(![]() ,
,![]() ,
,![]() )
)
则![]() ,
,![]() ,
,![]()
设平面PBC的法向量为![]() ,则
,则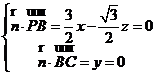 ,令x=1,则t=
,令x=1,则t=![]() ,故
,故![]() ,
,
设直线CE与平面PBC所成的角为θ,
则sinθ=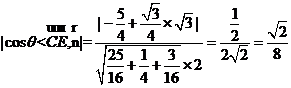
故直线CE与平面PBC所成角的正弦值为![]()
20.(本题满分15分)已知函数f(x)=(x–![]() )
)![]() (
(![]() ).
).
(Ⅰ)求f(x)的导函数;
(Ⅱ)求f(x)在区间![]() 上的取值范围.
上的取值范围.
【答案】(Ⅰ)f'(x)=(1-x)(1-![]() )
)![]() ;(Ⅱ)[0,
;(Ⅱ)[0, ![]()
![]() ].
].

(Ⅱ)令g(x)= x-![]() ,则g'(x)=1-
,则g'(x)=1-![]() ,当
,当![]() ≤x<1时,g'(x)<0,当x>1时,g'(x)>0,则g(x)在x=1处取得最小值,既最小值为0,又
≤x<1时,g'(x)<0,当x>1时,g'(x)>0,则g(x)在x=1处取得最小值,既最小值为0,又![]() >0,则f(x)在区间[
>0,则f(x)在区间[![]() ,+
,+![]() )上的最小值为0.
)上的最小值为0.
当x变化时,f(x),f'(x)的变化如下表:
x | ( | 1 | (1, |
| ( |
f'(x) | - | 0 | + | 0 | - |
f(x) | ↘ |
| ↗ |
| ↘ |
又f(![]() )=
)=![]()
![]() ,f(1)=0,f(
,f(1)=0,f(![]() )=
)=![]()
![]() ,
,
则f(x)在区间[![]() ,+
,+![]() )上的最大值为
)上的最大值为![]()
![]() .
.
综上,f(x)在区间[![]() ,+
,+![]() )上的取值范围是[0,
)上的取值范围是[0, ![]()
![]() ].
].
21.(本题满分15分)如图,已知抛物线![]() ,点A
,点A![]() ,
,![]() ,抛物线上的点
,抛物线上的点![]() .过点B作直线AP的垂线,垂足为Q.
.过点B作直线AP的垂线,垂足为Q.
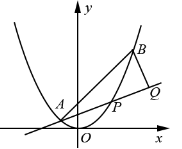
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求![]() 的最大值.
的最大值.
【答案】(Ⅰ)(-1,1);(Ⅱ)
【解析】解:(Ⅰ)由题易得P(x,x2),-![]() <x<
<x<![]() ,
,
故kAP=![]() =x-
=x-![]()
![]() (-1,1),
(-1,1),
故直线AP斜率的取值范围为(-1,1).
(Ⅱ)由(Ⅰ)知P(x,x2),-![]() <x<
<x<![]() ,
,
故![]() =(-
=(-![]() -x,
-x,![]() -x2),
-x2),
设直线AP的斜率为k,
则AP:y=kx+![]() k+
k+![]() ,BP:y=
,BP:y=![]() ,
,
由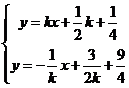
![]()
故![]() ,
,
又![]() ,
,
故![]() ,
,
即![]() ,令
,令![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() ,即
,即![]() 的最大值为
的最大值为![]() .
.
22.(本题满分15分)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*).
证明:当n∈N*时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1− xn≤![]() ;
;
(Ⅲ)![]() ≤xn≤
≤xn≤![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析.
(Ⅰ)证明:令函数![]() ,则易得
,则易得![]() 在
在![]() 上为增函数.
上为增函数.
又![]() ,若
,若![]() 恒成立
恒成立![]() ,
,
又由![]() 可知
可知![]() ,
,
由![]() .
.
所以![]() .
.
(Ⅱ)令![]() ,
,
则![]() ,
,
令![]() ,
,
则![]() ,所以
,所以![]() 单调递增.
单调递增.
所以![]() ,即
,即![]() ,
,![]() 单调递增.
单调递增.
所以![]() .
.
所以![]() .
.
即![]() .
.


2019年浙江高考数学科目已经结束了,同学们考的怎么样呢?为了方便大家了解自己的考试情况,小编为大家整理了2019年浙江高考数学试卷及参考答...

2019浙江高考理科数学科目的考试已经结束了,同学们都考的怎么样呢?小编为大家整理了2019年浙江高考理科数学试卷,供大家参考。2019年浙...

2019年浙江高考数学科目已经结束了,同学们考的怎么样呢?为了方便大家了解自己的考试情况,小编为大家整理了2019年浙江高考数学试卷及参考答...

2019年浙江高考数学科目已经结束了,同学们考的怎么样呢?为了方便大家了解自己的考试情况,小编为大家整理了2019年浙江高考数学试卷及参考答...

2018年浙江高考数学冲刺模拟试卷【含答案】

2017浙江高考数学压轴试题(含答案)